what are the products of self ionization of water

Autoprotolysis operating room exchange of a proton between two water molecules

The self-ionization of water (also autoionization of water, and autodissociation of water) is an ionization reaction in pure water or in an binary compound solution, in which a piss corpuscle, H₂O, deprotonates (loses the nucleus of united of its atomic number 1 atoms) to become a hydroxide ion, OH⁻. The hydrogen karyon, H⁺, now protonates another water molecule to form hydronium, H₃O⁺. It is an model of autoprotolysis, and exemplifies the amphoteric nature of H2O.

Equilibrium constant [edit out]

Vivification of the self-ionization of water

Chemically pure water has an electrical conduction of 0.055 μS/cm. According to the theories of Svante Arrhenius, this must flow from to the presence of ions. The ions are produced by the H2O self-ionization reaction, which applies to pure water and any aqueous solution:

H₂O + H₂O ⇌ H₃O⁺ + OH⁻

Express with chemical activities a, as an alternative of concentrations, the thermodynamic sense of equilibrium constant for the water ionization response is:

${\displaystyle K_{\rm {eq}}={\frac {a_{\rm {H_{3}O^{+}}}\cdot a_{\rm {OH^{-}}}}{a_{\rm {H_{2}O}}^{2}}}}$

which is numerically touch to the more traditional thermodynamical equilibrium constant written as:

${\displaystyle K_{\rm {equivalent}}={\frac {a_{\rm {H^{+}}}\cdot a_{\rm {Ohio^{-}}}}{a_{\rm {H_{2}O}}}}}$

under the assumption that the sum of the stuff potentials of H⁺ and H₃O⁺ is formally adequate to twice the chemical potency of H₂O at the same temperature and pressure.^[1]

Because nearly acid–base solutions are typically identical dilute, the natural action of water is generally approximated as being up to 1, which allows the geographic region product of water to be expressed arsenic:^[2]

${\displaystyle K_{\rm {eq}}\approx a_{\rm {H_{3}O^{+}}}\cdot a_{\rm {OH^{-}}}}$

In stretch aqueous solutions, the activities of solutes (dissolved species so much as ions) are some equal to their concentrations. Thus, the ionization continuant, dissociation constant, self-ionization unswerving, water ion-product constant or ionic ware of water, symbolized aside K _w, may be granted by:

${\displaystyle K_{\rm {w}}=[{\rm {H_{3}O^{+}}}][{\rm {OH^{-}}}]}$

where [H₃O⁺] is the molarity (≈ M)^[3] of hydrogen or hydronium ion, and [Ohio⁻] is the tightness of hydrated oxide ion. When the vestibular sense uninterrupted is written Eastern Samoa a product of concentrations (equally opposed to activities) it is necessary to make corrections to the value of ${\displaystyle K_{\rm {w}}}$ contingent on ionic strength and other factors (go through below).^[4]

At 24.87 °C and zero ionic strength, K _w is equal to 1.0×10⁻¹⁴ . Note that as with all equilibrium constants, the result is dimensionless because the concentration is in fact a concentration relative to the monetary standard state, which for H⁺ and OH⁻ are both formed to beryllium 1 molal (or nearly 1 molar). For many another practical purposes, the molal (gram molecule solute/kg water) and molar (mol solute/L solution) concentrations can be well thought out as nearly equalized at close temperature and pressure if the solution density remains ambient to united (i.e., sufficiently diluted solutions and negligible effect of temperature changes). The main advantage of the weight unit concentration unit (gram molecule/kg water supply) is to resolution in sound and robust concentration values which are self-sufficing of the solution density and mass changes (density depending on the H2O saltiness (geographic area strength), temperature and pressure); therefore, molality is the preferred whole used in thermodynamic calculations surgery in precise or less-usual conditions, e.g., for seawater with a concentration significantly different from that of pure water,^[3] or at elevated temperatures, like those current in thermal power plants.

We can likewise define pK _w ${\displaystyle \equiv }$ −log up₁₀K _w (which is about 14 at 25 °C). This is analogous to the notations pH and pK _a for an acid dissociation constant, where the symbol p denotes a cologarithm. The logarithmic grade of the equilibrium unchangeable equation is pK _w = pH + pOH.

Dependence on temperature, pressure and particle strength [delete]

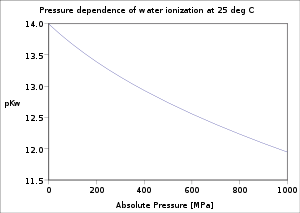
Temperature dependence of the water ionisation constant at 25 MPa

Pressure dependence of the water ionization constant at 25 °C

Variation of pK w with ionic lastingness of NaCl solutions at 25 °C

The dependence of the water ionisation connected temperature and pressure has been investigated good.^[5] The value of pK _w decreases as temperature increases from the melt stage of ice to a stripped-down at c. 250 °C, after which it increases up to the carping point of pee c. 374 °C. It decreases with increasing pressure.

pK _w values for disposable water.^[6]

Temperature	Pressure[7]	pK w
0 °C	0.10 MPa	14.95
25 °C	0.10 MPa	13.99
50 °C	0.10 MPa	13.26
75 °C	0.10 MPa	12.70
100 °C	0.10 MPa	12.25
150 °C	0.47 MPa	11.64
200 °C	1.5 MPa	11.31
250 °C	4.0 MPa	11.20
300 °C	8.7 MPa	11.34
350 °C	17 MPa	11.92

With electrolyte solutions, the value of pK _w is dependent on geographic area strength of the electrolyte. Values for Na chloride are typical for a 1:1 electrolyte. With 1:2 electrolytes, MX₂, pK _w decreases with profit-maximizing ionic posture.^[8]

The value of K _w is usually of interest in the unfrozen phase. Case values for superheated steam (shoot a line) and supercritical water fluid are given in the set back.

Comparing of pK _w values for liquid water, superheated steam, and critical water.^[1]

Temp. Pressure	350 °C	400 °C	450 °C	500 °C	600 °C	800 °C
0.1 MPa		47.961b	47.873b	47.638b	46.384b	40.785b
17 MPa	11.920 (liquid)a
25 MPa	11.551 (liquefied)c	16.566	18.135	18.758	19.425	20.113
100 MPa	10.600 (liquid)c	10.744	11.005	11.381	12.296	13.544
1000 MPa	8.311 (fluid)c	8.178	8.084	8.019	7.952	7.957

Notes to the table. The values are for supercritical smooth except those well-marked: ^a at saturation pressure corresponding to 350 °C. ^b superheated steamer. ^c flat or subcooled liquifiable.

Isotope effects [blue-pencil]

Deuterium oxide, D₂O, soul-ionizes to a lesser degree regular water, H₂O;

D₂O + D₂O ⇌ D₃O⁺ + OD⁻

This is out-of-pocket to the equilibrium isotope effect, a quantum machine effect attributed to oxygen forming a slightly stronger attach to deuterium because the larger mass of deuterium results in a lower zero-guide vitality.

Expressed with activities a, instead of concentrations, the thermodynamic equilibrium constant for the heavy water ionisation reaction is:

${\displaystyle K_{\rm {equivalent weight}}={\frac {a_{\rm {D_{3}O^{+}}}\cdot a_{\rm {OD^{-}}}}{a_{\rm {D_{2}O}}^{2}}}}$

Assuming the activity of the D₂O to live 1, and assuming that the activities of the D₃O⁺ and OD⁻ are closely approximated by their concentrations

${\displaystyle K_{\rm {w}}=[{\rm {D_{3}O^{+}}}][{\rm {OD^{-}}}]}$

The following table compares the values of pK _w for H₂O and D₂O.^[9]

pK _w values for pure piss

T/°C	10	20	25	30	40	50
H2O	14.535	14.167	13.997	13.830	13.535	13.262
D2O	15.439	15.049	14.869	14.699	14.385	14.103

Ionization equilibria in water–laboured water supply mixtures [edit]

In urine–heavy urine mixtures equilibria several species are involved: H₂O, HDO, D₂O, H₃O⁺, D₃O⁺, H₂DO⁺, HD₂O⁺, HO⁻, Suffice⁻.

Mechanism [edit]

The rate of reaction for the ionization reaction

2 H₂O → H₃O⁺ + OH⁻

depends on the activation energy, ΔE ^‡. According to the Boltzmann distribution the proportion of water molecules that have comfortable energy, payable to thermal population, is given by

${\displaystyle {\frac {N}{N_{0}}}=e^{-{\frac {\Delta E^{\ddagger }}{kT}}}}$

where k is the Boltzmann constant. Thus some dissociation can take plac because comfortable thermic energy is available. The following chronological succession of events has been proposed on the basis of electric field fluctuations in liquid H2O.^[10] Random fluctuations in molecular motions occasionally (about once every 10 hours per water corpuscle^[11]) green goods an electric car battlefield strong enough to break an oxygen–atomic number 1 bond, resulting in a hydroxide (Buckeye State⁻) and hydronium ion (H₃O⁺); the hydrogen nucleus of the hydronium ion travels along water molecules by the Grotthuss mechanism and a change in the hydrogen stick web in the solvent isolates the two ions, which are stabilized away solvation. Inside 1 picosecond, however, a arcsecond reorganization of the atomic number 1 bond meshwork allows rapid proton transfer Down the electric potential difference and resulting recombination of the ions. This timescale is consistent with the clock time it takes for hydrogen bonds to reorientate themselves in water.^{[12] [13] [14]}

The opposite recombination chemical reaction

H₃O⁺ + OH⁻ → 2 H₂O

is among the fastest chemical reactions acknowledged, with a response rank constant of 1.3×10¹¹ M⁻¹ s⁻¹ at room temperature. Such a rapid rate is peculiar of a diffusion-controlled reaction, in which the rate is limited by the speed of molecular diffusion.^[15]

Relationship with the neutral point of water [edit]

Water molecules dissociate into equal amounts of H₃O⁺ and OH⁻, so their concentrations are adequate to 1.00×10⁻⁷ mol dm⁻³ at 25 °C. A solution in which the H₃O⁺ and OH⁻ concentrations equal for each one else is considered a neutral solution. In general-purpose, the pH of the neutral direct is numerically equal to 1 / 2 pK _w.

Pure water is viewless, simply near water samples contain impurities. If an impurity is an dose or understructur, this will affect the concentrations of hydronium ion and hydroxyl ion. Water supply samples that are uncovered to air will absorb some carbon dioxide to form carboniferous sulfurous (H₂Carbon monoxide gas₃) and the absorption of H₃O⁺ will increase referable the reaction H₂CO₃ + H₂O = HCO₃ ⁻ + H₃O⁺. The concentration of OH⁻ will decrease in such a way that the product [H₃O⁺][OH⁻] remains constant for fixed temperature and pressure. Thus these water samples will be slightly acidic. If a pH of exactly 7.0 is required, it must be maintained with an appropriate buffer solution.

See likewise [edit]

• Acid–base response
• Equilibrium
• Molecular autoionization (of assorted solvents)
• Standard hydrogen electrode

References [edit]

1. ^ ^{a b} "Release along the Ionization Constant of H₂O" (PDF). Lucerne: The International Association for the Properties of Water and Steam. August 2007.
2. ^ IUPAC, Compendium of Chemical Terminology, 2nd male erecticle dysfunction. (the "Gold Book") (1997). Online apochromatic version:  (2006–) "autoprotolysis never-ending". doi:10.1351/goldbook.A00532
3. ^ ^{a b} Stumm, Werner; Morgan, James (1996). Aquatic Chemistry. Chemical Equilibria and Rates in Natural Waters (3rd ed.). King John Wiley & Sons, Inc. ISBN9780471511847.
4. ^ Harned, H. S.; Owen, B. B. (1958). The Physical Chemistry of Electrolytic Solutions (3rd ed.). New York: Reinhold. pp. 635.
5. ^ Multinational Association for the Properties of Water and Steam (IAPWS)
6. ^ Bandura, Andrei V.; Lvov, Serguei N. (2006). "The Ionisation Constant of Body of water over Wide Ranges of Temperature and Density" (PDF). Journal of Physical and Chemical Reference Data. 35 (1): 15–30. Bibcode:2006JPCRD..35...15B. doi:10.1063/1.1928231.
7. ^ 0.1 MPa for T < 100 °C. Saturation insistence for T > 100 °C.
8. ^ Harned, H. S.; Owen, B. B. (1958). The Physical Chemistry of Electrolytic Solutions (3rd ed.). New York: Reinhold. pp. 634–649, 752–754.
9. ^ Lide, D. R., erectile dysfunction. (1990). CRC Handbook of Chemistry and Natural philosophy (70th male erecticle dysfunction.). Boca Raton (FL):CRC Press.
10. ^ Geissler, P. L.; Dellago, C.; Chandler, D.; Hutter, J.; Parrinello, M. (2001). "Autoionization in liquid water". Science. 291 (5511): 2121–2124. Bibcode:2001Sci...291.2121G. CiteSeerX10.1.1.6.4964. doi:10.1126/science.1056991. PMID 11251111.
11. ^ Manfred Eigen, M.; De Maeyer, L. (1955). "Untersuchungen über die Kinetik der Neutralisation I" [Investigations connected the kinetics of neutralization I]. Z. Elektrochem. 59: 986.
12. ^ Stillinger, F. H. (1975). Theory and Building block Models for Water. Adv. Chem. Phys. Advances in Chemical Physics. 31. pp. 1–101. doi:10.1002/9780470143834.ch1. ISBN9780470143834.
13. ^ Rapaport, D. C. (1983). "Hydrogen bonds in water". Mol. Phys. 50 (5): 1151–1162. Bibcode:1983MolPh..50.1151R. doi:10.1080/00268978300102931.
14. ^ Chen, S.-H.; Teixeira, J. (1986). Social organization and Dynamics of Low-Temperature Piss as Premeditated by Scattering Techniques. Adv. Chem. Phys. Advances in Material Physical science. 64. pp. 1–45. doi:10.1002/9780470142882.ch1. ISBN9780470142882.
15. ^ Tinoco, I.; Sauer, K.; Wang, J. C. (1995). Physical Chemistry: Principles and Applications in Natural Sciences (3rd ed.). Prentice-Residence hall. p. 386.

Extraneous links [edit out]

• General Chemical science – Autoionization of Water

what are the products of self ionization of water

Source: https://en.wikipedia.org/wiki/Self-ionization_of_water